This is the first in a series of blog posts about how I wrote and optimized VkColors, a small compute program written using Vulkan.
During the summer between university semesters, I found a post on the Code Golf Stack Exchange. The challenge was to generate an image with all possible RGB colors, arranged however the contestant felt was best. The winner was Jozsef Fejes.
Jozsef’s program outputs the final image by saving a PNG file to disk. However, he provided a few GIFs that showed the image while the algorithm was running. That inspired me to write VkColors, a program that could generate those images as fast as possible and display them at 60 frames per second. I chose to use Vulkan because this was a good opportunity to use both the graphical and compute capabilities of the API.
The Algorithm
Jozsef places pixels using two algorithms that differ by scoring criteria. First, a queue of all colors is made and a single color is dequeued and placed in the center. A set of possible locations, the open set, is maintained. The open set contains any blank pixel next to a colored pixel (8 neighbors are considered). Then in a loop, the algorithm takes a single color from the queue, the new color, and evaluates a score for the new color against every location in the open set using the scoring criteria. All locations in the open set are considered each loop and the location with the lowest score is colored.
The first scoring criteria, which I call wave, scores a location based on the minimum of the differences between the new color and any already colored neighbors.

The second scoring criteria, which I call coral, scores a location based on the average of the differences between the new color and the already colored neighbors.
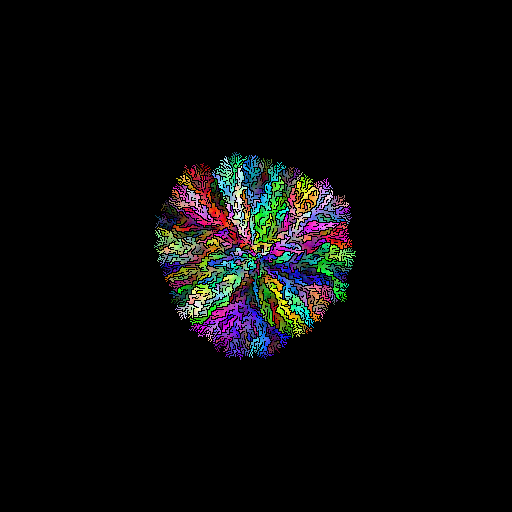
These two algorithms are the basis of VkColors. For this post, I will examine their performance from an algorithmic perspective and the performance of their CPU implementations. Later posts will examine their GPU implementations.
Algorithmic Analysis
If you look back at the picture for wave, you’ll see that it is solidly colored in and the outline is roughly circular. This is because wave scoring is not picky about which locations it chooses. If any of the 8 pixels around a possible location is close to the color being placed, that location gets a low score. There are a few places near the edge of the circle where some locations are uncolored and surrounded by colored locations, but these are unlikely to remain uncolored as the algorithm progresses.

The open set in wave is roughly circular with very few uncolored pixels within the circle. That means the size of the open set and the running time for one iteration is proportional to the diameter of the circle (at least until the circle grows into the edge of the image). For an n x n image, there are N pixels. One iteration has a running time of O(n) or O(sqrt(N)). There are N pixels in the queue, so the overall run time is O(n^3) or O(N^1.5).
For coral, the complexity is worse. Coral produces long, thin streaks of uncolored pixels between two colored areas. This is because it considers the average of all colored neighbors of a location. If a location has two neighbors that are colored differently, eg one is green and the other is red, that location will go uncolored for a long time. If the new color is also red, the algorithm will prefer to grow the circle outwards, rather than fill in the gap between the differently colored areas.

The open set in coral is roughly circular with many uncolored pixels within the circle. Those uncolored pixels are at a fairly uniform density for most of the algorithm’s run time. The complexity of one iteration is proportional to the area of the circle, O(n^2) or O(N). The overall run time is O(n^4) or O(N^2).
Implementation
VkColors is written in C++. To make it, I used a few libraries:
- GLFW for the windowing and event system
- GLM for vector and matrix types
- VulkanWrapper, which is my own C++ wrapper for Vulkan
From the start, VkColors needed to be able to generate pixels asynchronously from the rendering. Multiple pixels need to be produced for every frame that is displayed. If only one pixel was generated per frame, a 512×512 image would take 72 minutes to fully render at 60 FPS. This would be unacceptably slow. To solve this, VkColors uses two threads: one that generates pixels as fast as possible and one that renders the current state of the image at 60 FPS (or whatever the refresh rate of the user’s monitor is).
The generator thread has exclusive control over the state of the image, the open set, and the queue of colors. When it makes a chooses a location to color, it modifies the image and sends an update message to the render thread with the color and location chosen. The render thread has it’s own copy of the image that is updated by reading batches of update messages from the generator thread.
You can run this program yourself by building it from source or by using the provided Windows binaries in the Releases section on GitHub.
CPU Implementation
The generator thread is controlled by a virtual class Generator. The two algorithms are implemented on the CPU by the WaveGenerator and CoralGenerator classes and accessed by using the -generator=cpu-wave and -generator=-cpu-coral arguments. These are available under v1.0 in the git repo.
The performance of these implementations serve as a base line for the future GPU implementations. Performance was measured on my machine, which has an i3-4130 for the CPU and an RX 580 for the GPU. The measurements are for a 512×512 image.
The CPU wave generator placed 262,144 pixels in 28 seconds, which is 9362 pixels per second (pps). The algorithm hit a peak speed of ~40,000 pps at the start, when the radius of the circle of colored pixels is small. Then it fell steadily as the circle grew, until the circle hit the edge of the image, when it sped up as the corners were filled. The peak size of the open set was 2,646 locations.
The CPU coral generator took 1,439 seconds (~24 minutes) to place the same number of pixels, which is 182 pps. At the start, the algorithm ran at ~5,000 pps and it quickly fell down to ~100 pps. It did not speed up by much when the circle reached the edge of the image or even when the corners were mostly colored in. The streaks of uncolored pixels meant that the open set remained large until the algorithm was almost finished. The peak size of the open set was 73,584 locations.
These two measurements show the performance of the algorithm when implemented on the CPU. The GPU was barely stressed since it was only used to render a single image at 60 FPS. Later posts will explore how far I was able to push the performance by implementing the algorithms on the GPU.