I’ve been playing some roguelikes recently, so I wanted to try writing my own procedural dungeon generator. There are a lot of different ways to approach this problem, but I eventually decided to base mine off of TinyKeep’s algorithm, described here. I extended the algorithm to work in 3D, to create dungeons with multiple floors.
The code for this example is available in this Github repo. I’m using Unity3D for this demonstration, but these concepts are, of course, usable in any game engine.

Two Dimensions
First, I had to write the algorithm to work in two dimensions. It works mostly the same as the TinyKeep algorithm, but has been simplified in some ways (especially room generation) and is more complex in others.
The scene for this example is Dungeon2D. The code for this is in the Scripts2D folder.
The Algorithm
The world is divided into a rectangular grid. I assume that 1 unit is wide enough to represent a hallway. In a full game, 1 unit may correspond to 5 meters, for example. I chose a size of 30×30.
1. Place rooms arbitrarily such that they don’t overlap with each other. It doesn’t matter that much how they are arranged, so for this example, I’ve just placed and sized them randomly. I’ve also added a 1 unit wide buffer on each side (to ensure that rooms aren’t touching), but this is not required for the algorithm to work.

2. Create a Delaunay triangulation graph of the rooms. I used the Bowyer-Watson algorithm. There are many implementations for this algorithm in many languages. I selected one that was easy to translate into C#.
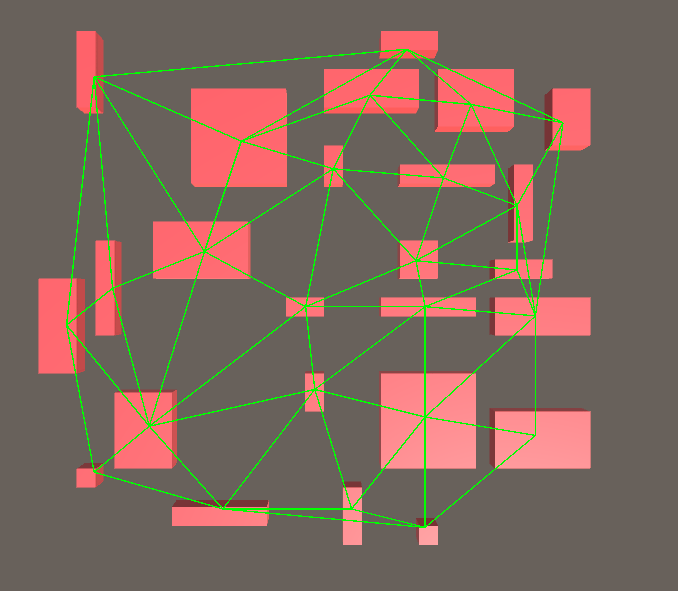
3. Create a minimum spanning tree (MST) from the triangulation. Here, I used Prim’s algorithm. The MST guarantees that every room will be reachable. However, since it is a tree, it contains no cycles. There is only a single path from one room to any other room.

4. Create a list of hallways, starting with every edge in the tree from Step 3. The tree contains every room, so it guarantees that a path to every room exists. Randomly add edges from the triangulation graph to the list. This will add some cycles to hallways. Here, I used a 12.5% chance for each edge to be added.
5. For every hallway in the list, use the A* algorithm to find paths from the start of a hallway to the end. After one path is found, it modifies the state of the world, so that future hallways can path around existing ones.
The cost function I used makes it cheaper to go through a hallway that another iteration carved, than to make a new hallway. This encourages the pathfinder to combine hallways that pass through the same area. Going through a room is possible, but expensive. So in most cases, the pathfinder will prefer to go around rooms.

Here’s some examples of this algorithm using actual art assets (the assets and the code to place them is not in the repo):


Three Dimensions
Now that I had a working dungeon generator in 2D, I started working to move it to 3D. All of the algorithms used have 3D versions, so it should be easy, right?
The Algorithm
The grid is now 30x5x30.
1. The first change was to generate rooms in 3D. This change was trivial.

2. Next, find the 3D Delaunay triangulation of the rooms, or rather the Delaunay tetrahedralization. Searching for either ” 3D Delaunay triangulation” or ” Delaunay tetrahedralization” returned a lot of research papers but no actual source code that I could find.
The closest was CGAL’s implementation of 3D triangulation, but there were two problems with it. One was that this module was only available under the GPL ????. The other was that the code was so heavily templated and inscrutable, that I didn’t actually find where they implemented the algorithm.
In the end, I had to learn how the Bowyer-Watson algorithm actually worked so I could change it myself. I still don’t really understand why circumcircles are so important, but I was at least able to write it using circumspheres instead, using this page from Wolfram MathWorld. Since it’s mostly 4×4 matrix operations I just used Unity3D’s Matrix4x4 type to do the heavy lifting.
This new version is in Scripts3D/Delaunay3D.cs, in case anyone else was looking for an MIT licensed, easy to understand version.

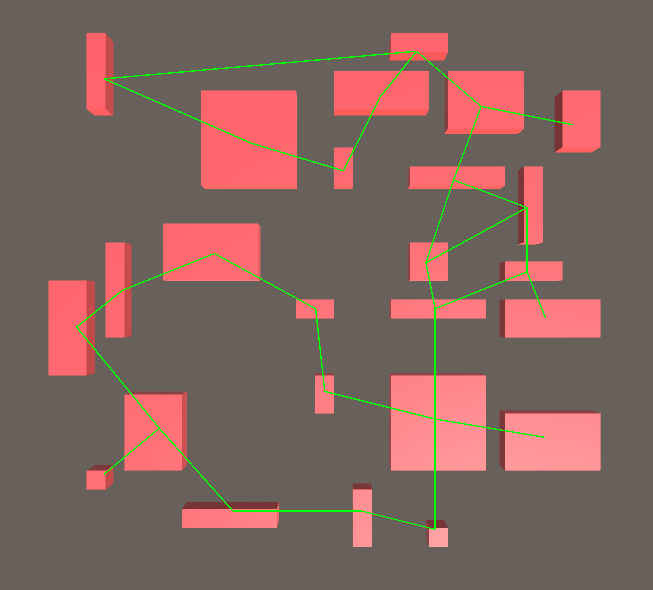
It’s hard to see, but instead of producing triangles with 3 vertices, the algorithm now produces tetrahedra with 4 vertices. At least one of those vertices will be on a different floor, otherwise the tetrahedron would be degenerate. This gives the pathfinding step plenty of opportunities to move between floors.
3 and 4. The edges from Step 2 can be fed into Prim’s algorithm with only trivial changes.


5. The 3D A* is where it gets complicated. The 2D version is the dead simple, standard implementation of A*. To make it 3D, I had to add the ability for the pathfinder to move up and down and connect rooms on different floors. I chose to connect floors using staircases rather than, say, a ladder.
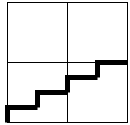
This is where the problem lies. A staircase is more complex than simply moving straight up. The staircase must move horizontally in order to move vertically. That is, there is a rise and a run. Consider the image below. The current cell is the solid blue square. The possible neighbors are the hollow squares. The pathfinder cannot move to the cell directly above the current cell. Instead, it has to move horizontally and vertically at the same time.

I had to choose the shape of the staircase in order to build a pathfinder for it. A rise to run ratio of 1:1 would be too steep, so I settled for a ratio of 1:2. It would move horizontally by two units for every vertical unit. Additionally, there must be headroom for characters to stand above the staircase itself, so the two cells directly above the staircase must be open as well. In total, there are four cells occupied by one staircase:
There must also be a hallway at the top and bottom of the stairs. The pathfinder cannot move into the staircase from the sides or the from the opposite direction. It would be impractical and look strange for a staircase to cut through a hallway like the images below.


So in the end, the staircase shape must look like the image below. The pathfinder must guarantee that the hallways at the two blue squares exist.
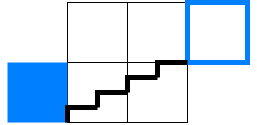
The pathfinder must move from the starting location to the end location in one step. This means it must move 3 units horizontally and 1 unit up or down. The A* algorithm is designed to move from one node to an adjacent node every step. To make staircases, I would need to “jump over” the four cells of the staircase.
The hard part is that I need to somehow make the pathfinder work around staircases that it creates. I can’t add them to the closed set of A*, since that would prevent a different path from going through those cells from a different direction. But I can’t leave them out, because then the pathfinder would be able to move through a staircase it just created, creating those unwanted situations pictured above.
The solution was for each node to keep track of all previous nodes in it’s path. Then when a neighbor node is being evaluated, it will be rejected if it falls on the path of the current node. The hallway at the end of the staircase would contain all of the cells occupied by the staircase, the node at the start of the staircase, and all nodes in the path before that, all the way to the start. The pathfinder could create another path that passes through the staircase, since the second path wouldn’t know about the staircase.
The above behavior is only for multiple potential paths within one call to the pathfinding function. There are still multiple pathfinding calls to generate all the hallways. Later iterations will just work around existing staircases like before.
The algorithm isn’t exactly A* at this point. There are too many special cases just to handle staircases. Having to check the entire previous path on each step is expensive. The naive implementation would be to follow the nodes all the way to the start, reading them like a linked list. That would make checking the path O(N), for every neighbor node.
The implementation I went with was to maintain a hashtable in each node that is keyed with the previous nodes. That makes checking the path O(1), but the hashtable must be copied when a node is added to the path, which is O(N). I chose this method because I figured that the algorithm would be reading paths more often than it modified them.
Either way, the overall complexity should be about O(N^2), though I don’t really know how to analyze it properly. This modification is the main bottleneck of the dungeon generation algorithm.
After all these changes are made, this is the result:



Here’s a 3D dungeon with actual art assets:

The dungeon generation algorithm can create some interesting emergent behavior.





Conclusion
The hardest part of this project was making the algorithms needed for the 3D version. I couldn’t find any implementations of 3D Delaunay triangulation, so I had to make one myself. The pathfinder’s requirements were very specific to my project, so I had to make it myself.
It was worth it. The dungeons created by this algorithm are interesting and might just make a basis for a good game.
1 thought on “Procedurally Generated Dungeons”
Comments are closed.